算法学习：归并排序以及插入排序

今天是大学第一个寒假的第一天，昨天玩了半天。

到了晚上临时起志：
既然上个暑假啥都没学精，那么这个寒假还是集中一个目标尽力往前进吧。
于是在B站上翻视频，一直到了23点。

今天找到了点生活的奔头，看了MIT学院的算法课程，又学习了两种排序方法，
虽然不像之前那么多事情了，如果有啥别的重要的话再说嘛，现在才第一天。
心里也想着，既然生活又有希望起来了，期待下学期的精彩旅途。
因为我一直都在说着：放假了就快开学了，
这样只看起点终点就很给人压迫，所以我还是喜欢去把每一天过得尽量好。

今天学习了归并排序（Merge Sort）与插入排序（Insertion Sort）
经过1-2小时的代码编辑，两种算法都已经以C语言实现完毕了，
这里就再复盘一下自己今天学习过的内容。
看到应该已经是第二天了，不过都一样。

1. 算法分析

对于一个算法，注重的是它的性能，性能并不是最重要的，
但在软件设计过程中，它充当着一种货币，可以通过损失性能来换取其他的特性。

一般来说，分析算法有三种方式：
1.最坏情况分析
2.平均值分析
3.最好情况分析

这里的情况指的是对于不同数据的运行时间，
我们认为时间T(n)与输入的数组大小n是一个相关映射。

最坏情况分析就是对于(1, n)下所有的输入中的时间最大值。
最好情况分析就是同理的最大值，但是并不一定反映程序运行的一般情况。

平均值严谨来说应该是时间期望，也就是每种情况的时间乘发生概率求和。
概率无从可知，所以我们需要假设一些概率分布模型。

2. 插入排序

1. 算法演示

   代码毕竟只是表达它而已，理解它能够让我们自己写出它来。

设想一个序列，我们用连续的小方格表示。
插入排序
从2开始遍历数组（假定下标从1开始），然后对于每一个元素进行上图的操作。
上图的操作，就好像是移动前面的元素，使得中间空出一个合适的位置，
然后将这个拿出来的key插入这个位置一样。

2. 代码表示
   对于一个下标从1到n的数组a

   1 2 3 4 5 6 7 8 9 10 11

   COPY for(int j = 2;j < n;j++) { key = a[j]; i = j - 1; while(a[i] > key && i > 0) { a[i + 1] = a[i]; i = i - 1; } a[i + 1] = key; }

实现的方法极其易懂，想记住打几遍代码也可以
道理就与上图中讲的类似。

当然，我们在C语言中的下标是从0开始的，
这样我们可以将j的初始值改变为1，将i的限定条件改为i >= 0
就可以对平常的C语言数组使用了。

3. 算法分析

一般来说，比较性能有两种方式：
一个是不同机器相同算法的相对速度
一个是不同算法相同机器的绝对速度

描述时间复杂度的符号有O、θ或者Ω，它们叫做渐进符号。
渐进分析是算法中的一个伟大的观点，
因为它不仅能够反映相对速度的大小，还能反映绝对速度的大小。
这些符号如何使用呢？

步骤
1.将一个式子中的低阶项去掉。
2.将最高阶的参数去掉。

比如一个式子 y = 3 * x^3 + 2 * x^2 （x^2即为x的平方）
去掉低阶项，则为y = 3 * x^3
去掉最高阶参数，则为θ(x^3).
（这个式子，是通过对于程序所有语句执行的次数累加的结果）

这就是我们说的时间复杂度刻画方式，实际上复杂度阶数大的时间并不一定大，
只是增长过程中一定能够找到超过复杂度阶小的时间的点，之后就一直比它大。
这是个临界点。

• 最坏情况分析
  对于这个算法，它的最坏情况即为完全逆序的情况，需要排序与移动项数n次，假设运行每一个语句的时间都是相等的常数C。

首先是一个2~n的循环，然后是一个从j - 1到0的循环

(j 2n)ΣjC C是一个常数，从1到n - 1.
这样jC也就是θ(j)，所以就变成了 (j 2n)Σθ(j)
因为每一项都是j * θ(j)，一共有n项，所以相当于θ(n ^ 2)

说实话，我不觉得排序是很高端的算法，甚至都不算算法。
至少在很久之前只知道选择与冒泡的时候是这样想的。
只觉得那些听不懂的，比如最短路径的迪杰斯特拉、二分查找、广度优先搜索这些才是。
实际上，面对这些较为简单的算法，我们反而更轻松地学习对于一个算法如何分析。

3. 归并排序

1. 算法演示

归并排序

这个算法看起来并不是很难，但是实现起来实在不容易，我这里是写了约90行代码。
它的道理就是，如果总共只有一个元素，那么就返回这个元素。
如果不是，就是两边先排序再归并，
归并方式就是挨个比，然后移除元素，直到所有元素都被移到排序后表。
实际上可以使用函数递归，这里还用的不熟练。

2. 代码演示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

int l = 0, i = 0, j = 0;
//i为a的下标，j位b的下标，l为c也就是排序后表的下标

while(1)
{
	//在表的最后一个元素没有被去掉的时候
	if(i != (n / 2) && j != n - (n / 2))
	{
		if(a[i] > b[j])
		{	
			c[l] = b[j];
			j += 1;
			l += 1;
		}
		else if(a[i] < b[j])
		{
			c[l] = a[i];
			i += 1;
			l += 1;
		}
		else if(a[i] == b[j])
		{
			c[l] = a[i];
			l += 1;
			c[l] = b[j];
			i += 1;
			j += 1;
			l += 1;
		}
	}
	//左表的最后一个元素被去掉
	else if(i == n / 2)
	{
		for(;j < n - (n / 2);j++)
			c[l++] = b[j];
		break;
	}
	//右表的最后一个元素被去掉
	else if(j == n - (n / 2))
	{
		for(;i < n / 2;i++)
			c[l++] = a[i];
		break;
	}
}

3. 算法分析
   对于这个算法，课程使用了递归树的模型
   对于两个表的排序，需要两个T(n/2)的时间，
   对于最后的归并，因为只是对于n个元素的操作，所以为θ(n)的时间。

最后的时间就是T(n) = 2 * T(n/2) + θ(n)

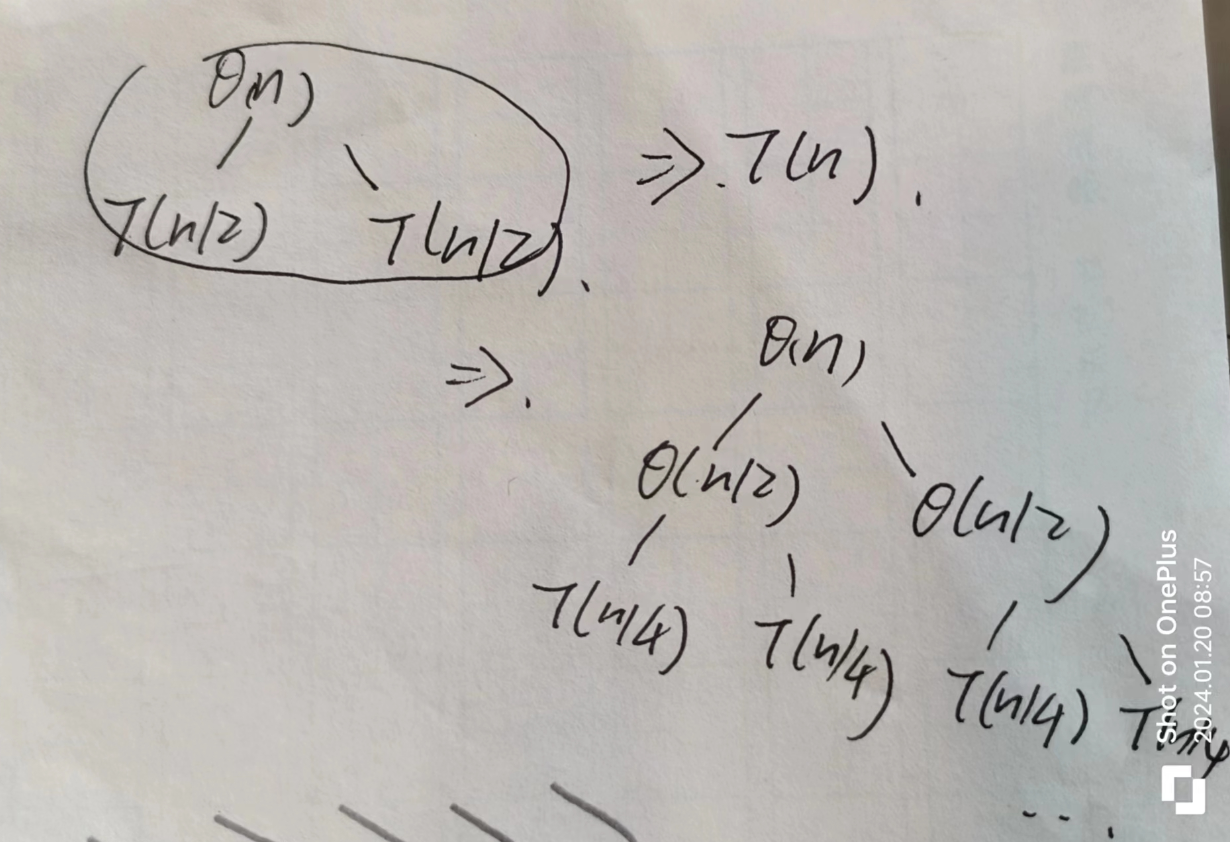递归树

递归树还没有整体学习，现在需要知道的就是，这个递归树的高度是log2n，最后的节点数是θ(n).
总共加起来等于θ(n) + logn * θ(n) 省去第一项就是θ(n * logn)，这样的话在性能上是优于插入排序的，而且它的临界点只在30左右，这也就是说归并排序在大多数情况下都是更快的。

开了个好头，总之希望好运，希望寒假快乐。

End…