算法学习：分治法中的二分查找

今天本应学习的是分治法，但今天的轨迹就是有点奇怪（哈）
我看着老师讲着讲着讲到了我可能接触过的算法了，并且Leetcode上还能够练题。
于是看完老师演示分治法的例子：归并排序、二分查找、求平方。
然后就开始不由自主地想要实现它，想了半天没有搞出来，查找网上才学会的。

今天也在Leetcode上练了几道有关于二分查找的题目，
开始的时候感觉 - 害，不就一个查找吗，直接当成函数，还能给我出什么题？！
尝试了一个困难难度的题根本做不出来（悲）
于是从简单题做起了，感觉知道了二分查找的很多不同的用法。

现在卡在了一道统计二叉树节点的题目上。
问题的关键是我现在不知道我这个想法对不对，
如果都是从1开始的话，那么其实不需要结构体与指针
其实就是在统计元素个数。
感觉想得过分简单了。

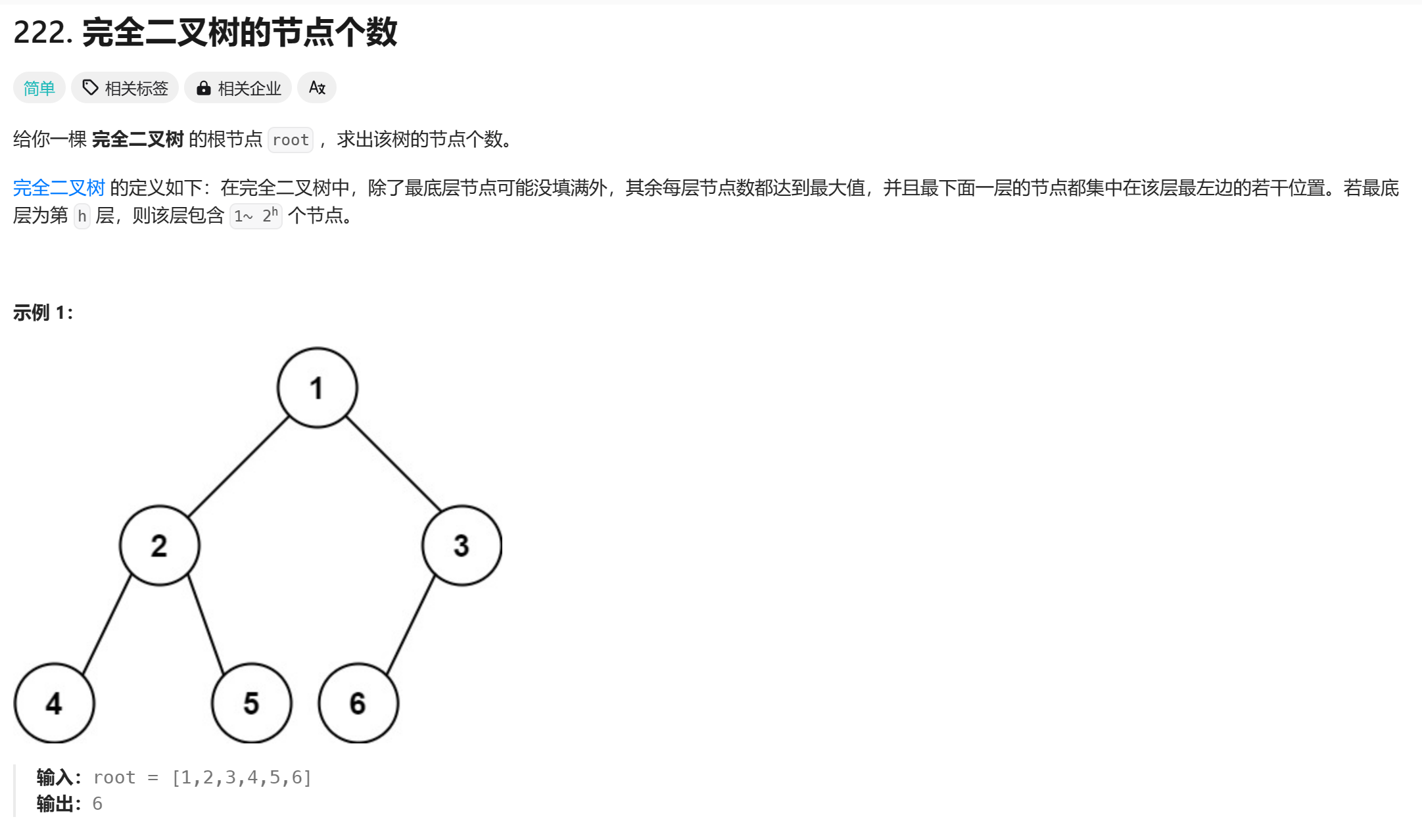题目

分治法还是一个挺笼统的概念，它不是一个算法，而是一个设计算法的方法。
主要可以分为三步：分、治以及组合。

老师使用了一个奇怪的比喻：
先将一块地分开成几个小部分，
分别统治它们，就相当于统治了这个总体。
不过还挺形象的。
我想起了函数的使用目的，也是为了拆分问题。

分也就是将一个问题划分成若干个小问题的过程。
治就是对于每一个问题进行解决的过程。
组合就是将这些小问题的答案组合形成最终的答案。
分治法衍生出的算法可能很多，但是它们的递归式基本都是相似的形式
也就是相似于主方法范式的那种。

比如 归并的 T(n) = 2 * T(n/2) + Θ(n)
二分的T(n) = T(n/2) + Θ(1)

接着就是上文讲到的那几个举例，也是我一天的轨迹转折的地方。

归并排序感觉现在已经不太想写了，
毕竟这个代码量与细节都挺复杂的，用qsort也挺好。
现在能够熟背的就是这个n^2的插入排序。
但是为了之后的效率我得尝试记忆一下更快的了

所以现在就说说二分查找吧，这是今天另一个值得讲的话题。

二分查找

1.算法演示

还是给出一个有序的数组，我们想要在这个数组中查找一个数字。
一般来说我们肯定最朴素的想法是一个n的循环遍历数组找这个数
但是这个算法真的挺快的，它的时间复杂度是Θ(logn)

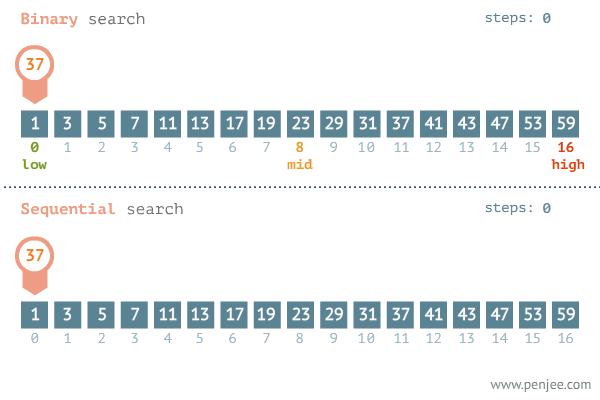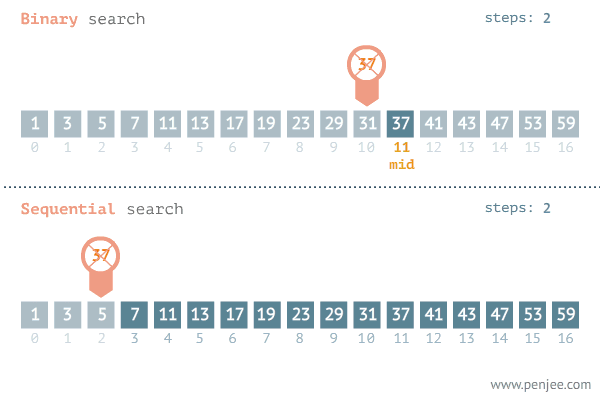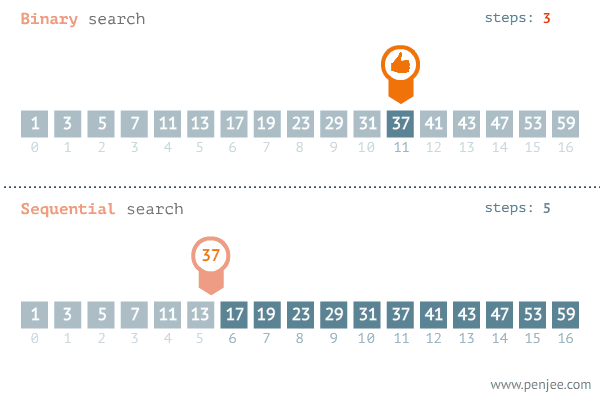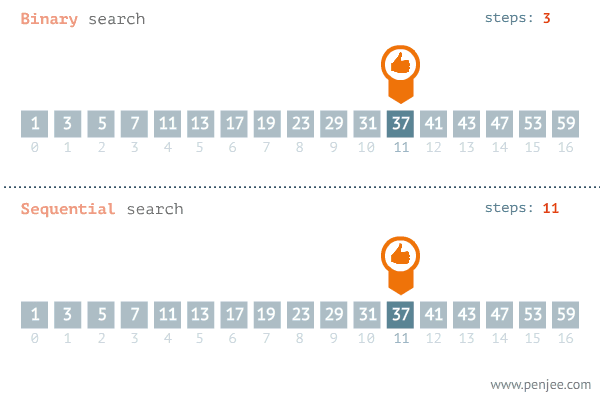来自于一个Python学习网站 www.penjee.com

用分治法的思路来想这个问题，

1.分 将一个数组分为大于中间数与小于中间数两部分。
2.治 如果搜索数小于中间数，去左边继续找
如果大于，去右边找。
3.混合，没啥操作。

在图中我们看到是通过low与high这两个变量来控制mid这个变量，
进而来确定我们数组的左边与右边。
%%说实话我刚开始就是卡在了这里，
我想用数组长度n来限定，想了很久没想出来右边怎么搞。%%

那么分别根据递归与它的定义，我们可以写出两种表示的形式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

int BinarySearch_Concept(int a[], int n, int x)
{
	int low = 0, high = n - 1, mid;
	while(low <= high)
	{
		mid = (low + high) / 2;
		if(x < a[mid])
			high = mid - 1;
		else if(x > a[mid])
			low = mid + 1;
		else return mid;
	} 
	return -1;
}

int BinarySearch_Recursion(int a[], int low, int high, int x)
{
	
	if(low > high) return -1;
	int mid = (low + high) / 2;
	//可以这样写 int mid = ((right - left) >> 1) + left;
	
	if(x == a[mid]) return mid;
	else if(x > a[mid])
	{
		low = mid + 1;
		return BinarySearch_Recursion(a, low, high, x);
	}
	else if(x < a[mid])
	{
		high = mid - 1;
		return BinarySearch_Recursion(a, low, high, x);
	}
}
//注 Concept为概念，Recursion为递归。

实际上只是一个思路两种写法而已，
这两种情况的执行时间应该是差不多的。

今天就是套这个模版然后改了点代码，
有的时候还超过了不少做过这道题的人。
空间复杂度上或者有时在时间复杂度上。
官方题解也不少可以学习的地方。

期望明天的学习，期望明天能够做出更多的题目，自己能够思考更多。